[백준1168] 요세푸스 문제2

[백준1168] 요세푸스 문제2 - Segment Tree

아, 그래요? 2022. 8. 12. 10:21

Segment Tree

#include <iostream>
#include <vector>

using namespace std;

vector<int> arr(12);
vector<int> tree(48);

int init(int idx, int start, int end) {
    if (start == end) return tree[idx] = arr[start];
    
    int mid = (start + end) /  2;
    
    return tree[idx] = init(idx*2, start, mid) + init(idx*2+1, mid+1, end);
}

void update(int node, int start, int end, int index, int diff) {
    if (!(start <= index && index <=end)) return;
    
    tree[node] += diff;
    
    if (start != end) {
        int mid = (start + end) / 2;
        update(node * 2, start, mid, index, diff);
        update(node * 2 + 1, mid+1, end, index, diff);
    }
}

int sum(int node, int start, int end, int left, int right) {
    if (left > end || right < start) return 0;
    
    if (left <= start && end <= right) return tree[node];
    
    int mid = (start + end) / 2;
    return sum(node*2, start, mid, left, right) + sum(node*2+1, mid+1, end, left, right);
    
}

int getIdxBySum(int val, int node, int start, int end) {
    if (start == end) return start;
    
    int mid = (start + end) / 2;
    if (val <= tree[node*2]) {
        return getIdxBySum(val, node*2, start, mid);
    } else {
        return getIdxBySum(val-tree[node*2], node*2+1, mid+1, end);
    }
}

init

init(int node, int start, int end)

정의 : Segment Tree를 만드는 함수
매개변수 : node를 시작으로 arr의 start~end 인덱스의 값들로 세그먼트 트리를 만듦.
기저 (base) : start와 end의 값이 같은 경우 → node위치의 노드(tree[node])에 arr[start]값 할당
재귀 (recursive) :
- 왼쪽 자식노드(node*2)에 범위의 절반에 값(start~mid)으로 세그먼트 트리를 만듦
- → init(node*2, start, mid)
- 오른쪽 자식노드(node*2+1)에 범위의 절반의 값(mid+1~start)으로 세그먼트 트리를 만듦
- → init(node*2+1, mid+1, end)
- 둘을 합침.

update

void update(int node, int start, int end, int index, int diff)

정의 : arr의 index위치의 값을 diff 만큼 변경시켜 세크먼트 트리를 업데이트
매개변수 정의 :
- node는 현재 노드의 위치이고, start~end가 현재 노드의 부분합 범위.
- index는 값을 바꿀 arr의 위치이고, diff는 변경할 크기
기저 (base) :
- 바꿀 값의 위치가 현제 노드의 부분합 범위(start~end)를 벗어나 있는 경우
- → 업데이트 할 필요 없으므로 그냥 리턴.
재귀 (recursive) :
- 일단 노드 범위에 변경값이 있으므로 현재 노드 값을 diff 만큼 업데이트
- 현재 노드가 리프노드(start=end)인 경우, 함수 종료
- 아닌경우, 왼쪽 자식노드와 오른쪽 자식노드에 업데이트 실행
  - 왼쪽 자식노드 → update(node*2, start, mid, index, diff)
  - 오른쪽 자식노드 → update(node*2+1, mid+1, end, index, diff)

sum

int sum(int node, int start, int end, int left, int right)

정의 : start~end 구간에서 left~right 구간의 부분합을 구함.
매개변수 :
- node는 현재 노드이고 start~end는 현재 노드의 부분합 범위.
- left~right는 구하고 싶은 부분합 범위.
- sum 함수는 주어진 구간(start~end)내에서 left~right중 포함되는 부분만 계산
  - 만약, [left, right]가 아예 범위 내에 없을 경우 0을 리턴
  - 일부만 있을경우, 그 일부의 합만 리턴
기저(base) :
- 구하려는 부분합의 범위가 주어진 범위 밖에 있는 경우 → 0
- 구하려는 범위가 주언진 범위를 포함하는 경우 → 주어진 범위의 부분합 : tree[node]
재귀 :
- 구하려는 부분합 범위가 주어진 범위 내에 있거나 일부 포함되어 있을경우 재귀탐색을 해야함.
- 왼쪽 자식노드에서의 부분합과 오른쪽 자식노드에서의 부분합을 더하면 됨.
- → sum(node2, start, mid, left, right) + sum(node2+1, mid+1, end, left, right)

getIdxBySum

int getIdxBySum(int val, int node, int start, int end)

정의 : arr[0]~arr[k]의 합이 val이 되게 하는 k 구하기
매개변수 :
- val은 주어진 부분합
- node는 현재 노드이고, start~end는 node의 부분합 범위
기저(base) :
- 리프노드(start=end)인 경우 → 현재 노드까지의 부분합이 자동으로 val이 됨 → start 리턴
재귀 :
- 두가지 경우가 존재함. arr[k]에 해당하는 리프노드가 왼쪽에 있는 경우, 오른쪽에 있는 경우
  - 왼쪽 서브트리에 있는 경우 → getIdxBySum(val, node*2, start, mid)
  - 오른쪽 서브트리에 있는경우, 왼쪽의 서브트리의 부분합까지 포함하고 있으므로, 해당 합을 빼고, 구해야함. → getIdxBySum(val-tree[node2], node2+1, mid+1, end)

요세푸스 문제

O(NK) solution

단순하게 생각하면 K번째 수를 탐색하는 동작을 N번 반복하면 된다. 탐색을 완전탐색으로 하면 1번 할때마다 O(K)의 복잡도가 발생하고 N번 반복하므로 해당 솔루션의 시간복잡도는 **O(NK)**이다.

큐 자료구조를 사용하면 쉽게 구현할 수 있다.

#include <iostream>

using namespace std;

int solution(int* arr, int n, int k) {
	
	queue<int> q;
	for (int i=0; i<n; ++i) q.push(arr[i]);

	cout << "<";
	for (int i=0; i<n-1; ++i) {	
		for (int j=0; j<k-1; ++j) {
			int cur = q.top(); q.pop();
			q.push(cur);
		}
		cout << q.top() << ", ";
		q.pop();
	}
	cout << q.top() << ">";
}

O(NK)로 문제를 해결할 경우, 최악의 경우 100억번의 연산이 필요하다 → 시간초과

O(NlgN) Solution

N번 숫자를 빼내야 하므로 N번 반복하는 것을 더 줄이는 것은 어렵다. 그렇기 때문에 탐색하는 과정을 기존의 O(K)에서 O(lg…) 수준으로 줄여야 한다. 그러기 위해 사용하는 것이 세그먼트 트리이다.

[ 세그먼트 트리 ]

솔루션에서 사용할 세그먼트 트리는 다음과 같다.

arr의 index가 리프노드(leaf node)
리프노드는 대응하는 index의 값이 존재할경우 1, 이미 제거했을 경우 0

N=7인 경우를 살펴보자.

모든 인덱스의 값이 그대로 있으므로 리프노드는 모두 1이다.

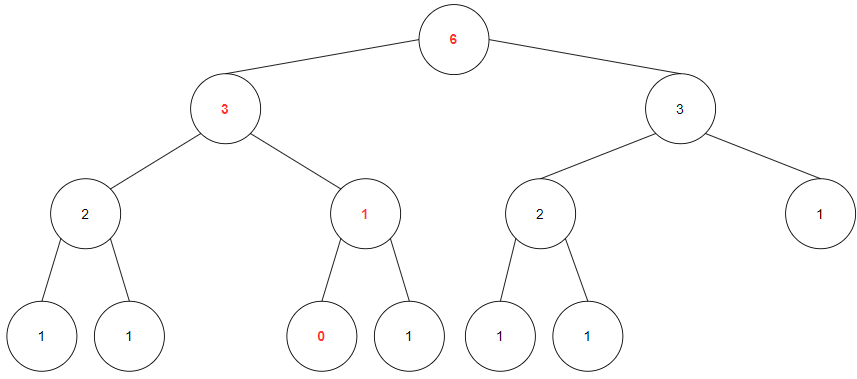
만약 3번째 값이 제거되었을 경우 트리는 아래와 같이 변경된다.

세번째 리프노드가 0이되고, 이에따라 부모 노드들이 모두 업데이트 된다.

[ 아이디어 ]

요세푸스 문제의 핵심은 현재 제거한 노드의 다음 노드를 기준으로 K번째 노드를 찾는 것이다. 이것을 위에 표현한 세그먼트 트리에 적용해보면 0이 된 노드의 다음노드부터 몇번째 노드까지의 합이 k인지를 구하는 문제이다.

[ 구현 ]

위에 구현한 세그먼트 트리에서 1번째 노드부터 K번째 노드까지의 합이 주어졌을때 K를 구하는 메서드인 getIdxBySum 메서드가 있으므로 아래의 방법으로 다음 출력할 노드를 구할 수 있다.

1번 노드부터 현재 출력한 노드 (처음일 경우, 시작 노드)까지의 부분합을 구함.
1번 노드부터 다음 출력할 노드까지의 합은 1.에서 구한 값의 k를 더한 값이므로 해당 값을 기반으로 getIdxBySum 함수를 통해 출력 노드를 구함.

int prev_sum = sum(1, 1, n, 1, prev);

int next_idx = getIdxBySum(prev_sum+k, 1, 1, n);
update(1, 1, n, next_idx, -1);
cout << next_idx << ", ";
prev = next_idx;

코드로 보면,

prev_sum은 1번노드부터 현재 출력한 노드까지의 합이 할당됨.
그 값에 k를 더해 다음 노드인 next_idx를 구해서 출력.
next_idx에 해당하는 노드가 제거되었으므로 해당 리프노드의 값을 0으로 변경하고 트리를 업데이트.
prev의 현재 출력한 노드를 저장

원형이어서 생기는 문제

우리가 사용하는 arr 배열은 선형이지만, 실제 문제에서 수열은 원형으로 주어져있다. 즉, N다음에 1로 넘어가야 한다.

예를 들어 N=7, K=3이라고 해보자. 3번노드가 지워지고, 그다음은 6번노드가 지워진다. 그다음은 어떻게 될까? 만약 위에 설명한 알고리즘으로 구현해본다면 다음과 같이 될것이다.

1~6번 리프노드의 부분합 = 4 (현재 4개의 노드만 남아있음), k=3
합이 7이므로 1번노드부터 몇번노드까지 더해야 7인지 구함 → 값이 없음! (노드 5개밖에 안남음)

이때 7이 의미하는 것은 결국 남은 5개의 노드를 모두 돌고, 다시 2번째 노드이다. 즉, 원형에 대응하기 위해서는 추가적으로 전체 노드를 순회하는(한바퀴를 도는) 것에 대해서 구현해주어야 한다.

while (prev_sum + k > tree[1]) {
    prev_sum -= tree[1];
}

코드를 보면, 부분합이 현재 노드의 개수(tree[1])보다 큰 경우 남은 노드의 개수를 빼줌으로써, 노드 전체를 한바퀴도는 효과를 발생시킨다.

[ 시간복잡도 ]

크게 두가지 과정을 N번 반복한다.

부분합을 구하는 과정(sum) → O(lgN)
부분합을 통해 다음 노드를 구하는 과정(getIdxBySum) → O(lgN)

즉 시간복잡도는 O(NlgN)이다.

최종 Solution

#include <iostream>
#include <vector>

using namespace std;

vector<int> arr;
int tree[400004];

int init(int idx, int start, int end) {
    if (start == end) return tree[idx] = arr[start];
    
    int mid = (start + end) /  2;
    
    return tree[idx] = init(idx*2, start, mid) + init(idx*2+1, mid+1, end);
}

void update(int node, int start, int end, int index, int diff) {
    if (!(start <= index && index <=end)) return;
    
    tree[node] += diff;
    
    if (start != end) {
        int mid = (start + end) / 2;
        update(node * 2, start, mid, index, diff);
        update(node * 2 + 1, mid+1, end, index, diff);
    }
}

int sum(int node, int start, int end, int left, int right) {
    if (left > end || right < start) return 0;
    
    if (left <= start && end <= right) return tree[node];
    
    int mid = (start + end) / 2;
    return sum(node*2, start, mid, left, right) + sum(node*2+1, mid+1, end, left, right);
    
}

int getIdxBySum(int val, int node, int start, int end) {
    if (start == end) return start;
    
    int mid = (start + end) / 2;
    if (val <= tree[node*2]) {
        return getIdxBySum(val, node*2, start, mid);
    } else {
        return getIdxBySum(val-tree[node*2], node*2+1, mid+1, end);
    }
}

int main() {
    int n;
    int k;
    
    cin >> n >> k;
    for (int i=0; i<=n; ++i) {
        arr.push_back(1);
    }

    init(1, 1, n);
    
    int prev = 0;
    cout << "<";
    for (int i=0; i<n-1; ++i) {
        
        int prev_sum = sum(1, 1, n, 1, prev);
        
        while (prev_sum + k > tree[1]) {
            prev_sum -= tree[1];
        }
        int next_idx = getIdxBySum(prev_sum+k, 1, 1, n);
        update(1, 1, n, next_idx, -1);
        cout << next_idx << ", ";
        prev = next_idx;
    }

	  int next_idx = getIdxBySum(1, 1, 1, n);
    cout << next_idx << ">";
}