[백준1517] 버블소트

아, 그래요? 2022. 8. 27. 20:02

정렬되지 않은 수열을 버블정렬 하는 과정에서 스왑이 몇번 일어나는지 출력하는 간단한 문제이다.

O(N^2) Solution

ll bubbleSort(int n) {
    
    ll ret = 0;
    
    for (int i=0; i<n; ++i) {
        for (int j=0; j<n-1-i; ++j) {
            if (bubbleArr[j] > bubbleArr[j+1]) {
								// SWAP
                ret++;
                int tmp = bubbleArr[j+1];
                bubbleArr[j+1] = bubbleArr[j];
                bubbleArr[j] = tmp;
            }
        }
    }
    
    return ret;
}

직관적으로 직접 버블 정렬을 하면서 스왑 횟수를 카운트할 수 있다.
버블 정렬의 시간복잡도인 O(N^2)의 시간복잡도를 가진다. 그런데 주어진 입력범위가 510^5만이므로 시간복잡도는 2.510^11이다. 이는 실행시간 1초를 아득히 넘긴다 → 시간초과

O(NlgN) Solution

이 문제를 해결하기 위해서는 버블 정렬보다 더 빠른 정렬 알고리즘을 사용해야 한다.
버블 정렬보다 더 빠른 정렬은 병합 정렬(Merge Sort, 머지소트)이다.
병합 정렬 과정에서 어떻게 스왑 횟수를 구할 수 있을까?

[버블 정렬에서 스왑이 일어나는 이유]

우리가 이 문제에 접근하기 위해서는 병합 정렬에서 어떤 시점에 스왑이 일어나는지 알아야한다. 병합 정렬은 두 수에 대해 크기의 순서와 index의 순서가 다를 경우(**x<y인데, arr[x]>arr[y]**인 경우) 스왑을 한다.

즉, 다른 정렬을 사용하더라도, 크기의 순서와 index의 순서가 다른 경우를 포착하여 이 경우를 카운트해주면 버블 정렬의 스왑횟수를 구할 수 있다.

그렇다면 병합 정렬에서 크기의 순서와 index의 순서가 달라서 스왑이 일어나는 순간을 포착할 수 있는 타이밍은 언제일까? 바로 병합(merge)을 하는 순간이다.

실제 정렬된 두 수열을 병합하는 과정에서 스왑횟수를 구하는 예제를 보자.

위 그림은 정렬된 두 수열을 병합(merge)하여 빈 수열에 삽입한다. 차례대로 오른쪽 수열에서 1,2가 들어 갔을거고, 3이 삽입되는 시점을 생각해보자. 3은 기존의 수열에서 1,2보다 앞에 있었다. 그런데 정렬된 수열에서는 1,2보다 뒤로 가게된다. 즉, 2번의 스왑이 필요한 것이다.

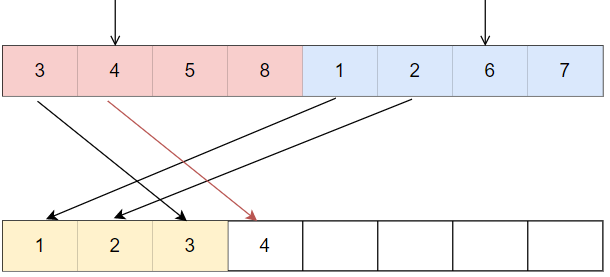
그 다음 상황을 보자. 이번에는 4가 1,2,3 다음으로 삽입이 된다. 이때 4는 3보다 ‘원래’ 뒤에 있었으므로 스왑이 일어나지 않지만,

1,2보단 앞에 있었으므로 2번의 스왑이 일어난다.

같은 방식으로 끝까지 정렬을 수행하면, 5는 2번의 스왑, 6,7은 더 앞으로 이동하므로 스왑이 일어나지 않고, 8은 1,2,6,7보다 원래 앞에 있었으므로 4번의 스왑이 일어난다. 즉, 총 2+2+2+4=10번의 스왑이 일어난다.

그리고 이 값은 정렬전 수열과 정렬 후 수열의 같은 수를 선으로 이었을때 교차점의 개수와 같다

코드로 구현하면 아래와 같다.

ll merge(int l, int m, int r) {
    
    int left = l;
    int right = m+1;
    int curr = left;
    
    ll ret = 0;
    ll cnt = 0;
    
    while (left <= m && right <= r) {
        
        if (arr[left] <= arr[right]) {
            sortArr[curr++] = arr[left++];
            ret += cnt;
        } else {
            sortArr[curr++] = arr[right++];
            cnt++;
        }
    }
    
    while (left <= m) {
        sortArr[curr++] = arr[left++];
        ret += cnt;
    }
    
    while (right <= r) {
        sortArr[curr++] = arr[right++];
    }
    
    for (int i=l; i<=r; ++i) {
        arr[i] = sortArr[i];
    }
    
    return ret;
}

병합 정렬의 특성상 두 수열을 병합할때 오른쪽의 수열은 본인의 위치보다 더 뒤로 가지 않는다.
즉, 뒤로 가는 경우를 기준으로 스왑 횟수를 카운트할 경우, 스왑 카운트는 왼쪽 수열의 수가 삽입되는 타이밍에만 하면 된다.
왼쪽 수열의 수가 삽입될때, 일어나는 스왑 횟수는 이미 삽입된 오른쪽 수열의 수 개수이다.
(나보다 뒤에 있었으나, 앞에 삽입된 수의 개수)
cnt는 현재까지 삽입된 오른쪽 수열의 수이다.
왼쪽 수열의 수가 삽입될때 이미 삽입된 오른쪽 수열의 수 만큼 스왑이 일어나므로 cnt를 ret(리턴값)에 더해주면 된다.

ll mergeSort(int l, int r) {
    
    if (l == r) return 0;
    
    ll ret = 0;
    int m = (l + r) / 2;
    
    ret += mergeSort(l, m);
    ret += mergeSort(m+1, r);
    
    return ret += merge(l, m, r);
}

최종적으로 정렬의 스왑횟수는 오른쪽 수열 정렬에서의 스왑횟수와 왼쪽 수열 정렬에서의 스왑횟수에 두 수열의 병합과정에서의 스왑횟수를 더하면 된다.

Solution

#include <iostream>
#include <vector>

using namespace std;

using ll = long long;

vector<int> arr(500000);
vector<int> sortArr(500000);

// l~m / m+1~r
ll merge(int l, int m, int r) {
    
    int left = l;
    int right = m+1;
    int curr = left;
    
    ll ret = 0;
    ll cnt = 0;
    
    while (left <= m && right <= r) {
        
        if (arr[left] <= arr[right]) {
            sortArr[curr++] = arr[left++];
            ret += cnt;
        } else {
            sortArr[curr++] = arr[right++];
            cnt++;
        }
    }
    
    while (left <= m) {
        sortArr[curr++] = arr[left++];
        ret += cnt;
    }
    
    while (right <= r) {
        sortArr[curr++] = arr[right++];
    }
    
    for (int i=l; i<=r; ++i) {
        arr[i] = sortArr[i];
    }
    
    return ret;
}

ll mergeSort(int l, int r) {
    
    if (l == r) return 0;
    
    ll ret = 0;
    int m = (l + r) / 2;
    
    ret += mergeSort(l, m);
    ret += mergeSort(m+1, r);
    
    return ret += merge(l, m, r);
}

int main() {
    int n;
    cin >> n;
    
    for (int i=0; i<n; ++i) {
        cin >> arr[i];
    }
    
    cout << mergeSort(0, n-1);
    
}